透视的原理

单点透视

根据常识我们可以知, 走廊两边的墙一般是平行的直线, 但在摄影作品中我们会发现, 体现在照片中的走廊趋势并不是平行的, 具体体现

画一下透视可以看出

所有物理上不平行于视线的线, 延长后最终趋近于一点, 本文是探讨一下为什么会出现这种结果.

设这么一个场景

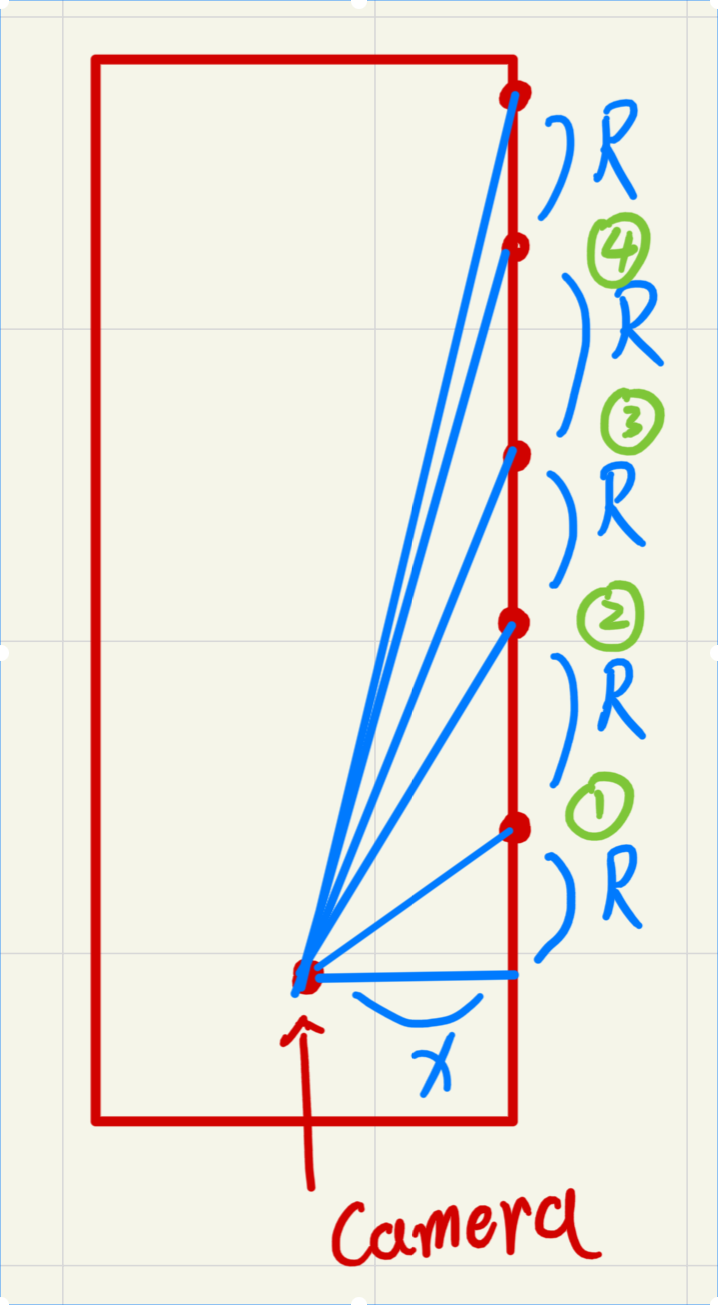
已知摄像机位置, 也就是漫画中我们读者的视角或者照片中相机所在的位置.

其距离1点的物理距离为 $L_1=\sqrt{x^2+R^2}$ , 距离2点则为$L_2=\sqrt{x^2+(2R)^2}$, 即距离n点的位置为$L_n=\sqrt{x^2+(nR)^2}$, x固定不变, 当n逐渐增大的时候, $\lim\limits_{\substack{n\to\infty }} L_n=nR$, x可以忽略不计, 此时两点的距离(图中橙色的部分)

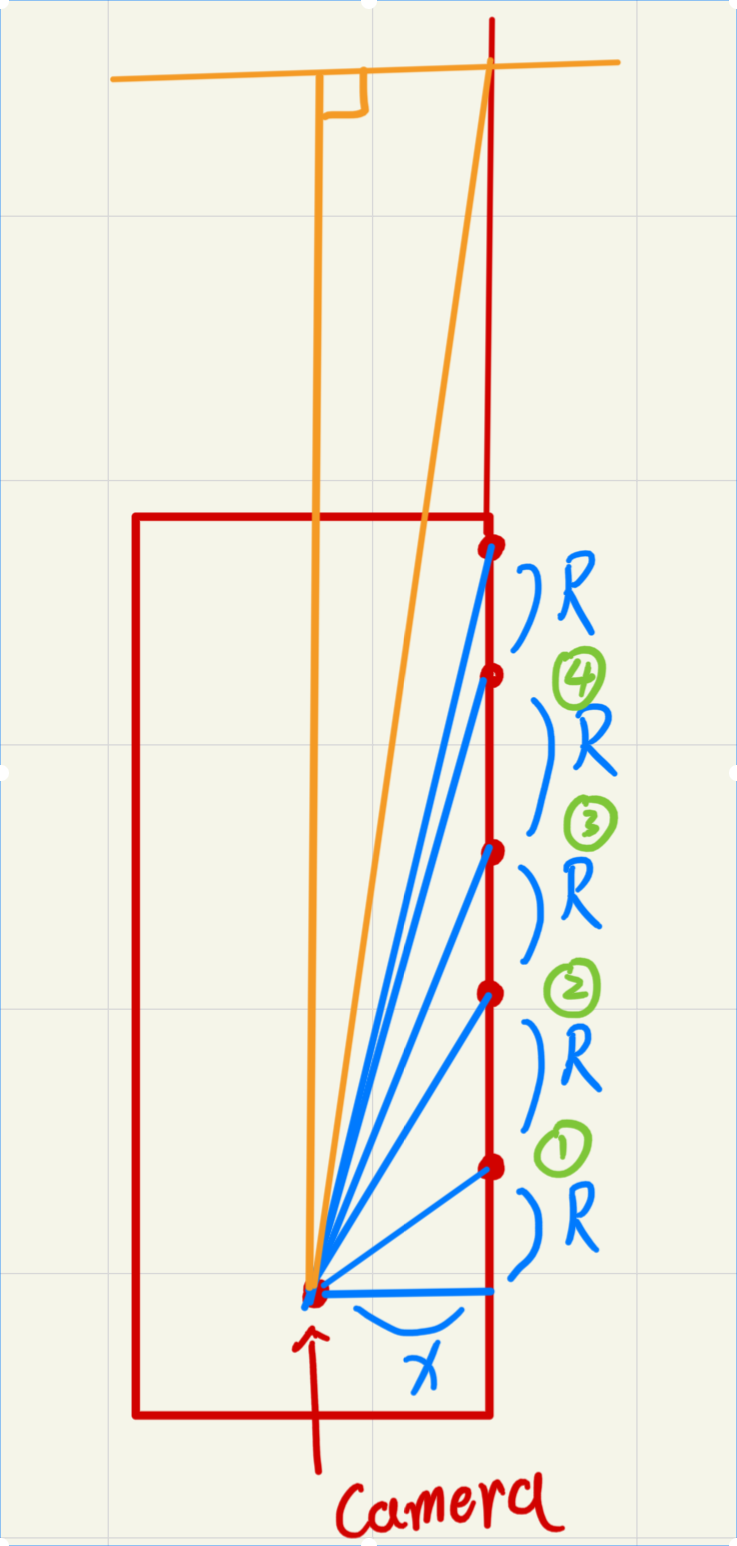
两个橙色的长度在极限距离可以视作相等, 根据上述距离公式$L_n=\sqrt{x^2+(nR)^2}$(自变量为$n$)可以知道, 此函数一阶导数为$L_n’=\dfrac{R^2}{\sqrt{\dfrac{x^2}{n^2}+R^2}}$, 随着n的增大, 导数值逐渐变大, 最终趋向1, 即最终L最终等于R(常数),